JavaScript 中的树型数据结构
实现和遍历技术
作者:Anish Kumar 译者:同学小强 来源:stackfull
Tree 是一种有趣的数据结构,它在各个领域都有广泛的应用,例如:
- DOM 是一种树型数据结构
- 我们操作系统中的目录和文件可以表示为树
- 家族层次结构可以表示为一棵树
树有很多变体(如堆、 BST 等) ,可用于解决与调度、图像处理、数据库等相关的问题。许多复杂的问题可能看起来和树没有关系,但是实际上可以表示为一个问题。我们还将讨论这些问题(在本系列后面的部分中) ,看看树是如何使看似复杂的问题更容易理解和解决的。
引言
为二叉树实现一个1
2
3
4
5
6
7
8
9
10
11
```js
function Node(value){
this.value = value
this.left = null
this.right = null
}
// usage
const root = new Node(2)
root.left = new Node(1)
root.right = new Node(3)
因此,这几行代码将为我们创建一个二叉树,它看起来像这样:
1 | 2 |
这很简单。现在,我们如何使用这个呢?
遍历
让我们从试图遍历这些连接的树节点(或整颗树)开始。就像我们可以迭代一个数组一样,如果我们也可以“迭代”树节点就更好了。然而,树并不是像数组那样的线性数据结构,因此遍历这些数据结构的方法不止一种。我们可以将遍历方法大致分为以下几类:
- 广度优先遍历
- 深度优先遍历
广度优先搜索/遍历(BFS)
在这种方法中,我们逐层遍历树。我们将从根开始,然后覆盖所有的子级,以及覆盖所有的二级子级,以此类推。例如,对于上面的树,遍历会得到如下结果:
1 | 2, 1, 3 |
下面是一个略微复杂的树的例子,使得这个更容易理解:
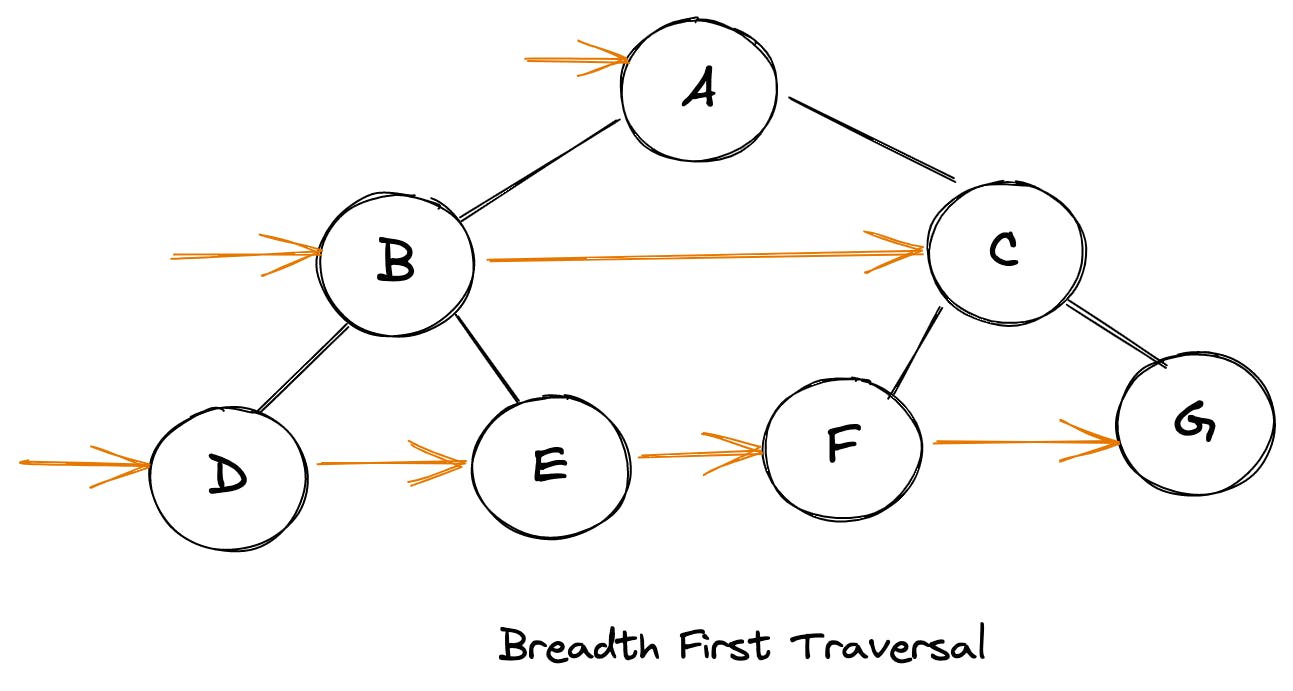
要实现这种形式的遍历,我们可以使用一个队列(先进先出)数据结构。下面是整个算法的样子:
- 初始化一个包含 root 的队列
- 从队列中删除第一项
- 将弹出项的左右子项推入队列
- 重复步骤2和3,直到队列为空
下面是这个算法实现后的样子:
1 | function walkBFS(root){ |
我们可以稍微修改上面的算法来返回一个二维数组,其中每个内部数组代表一个包含元素的层级:
1 | function walkBFS(root){ |
深度优先搜索/遍历(DFS)
在 DFS 中,我们取一个节点并继续探索它的子节点,直到深度到达完全耗尽。这可以通过以下方法之一来实现:
1 | root node -> left node -> right node // pre-order traversal |
所有这些遍历技术都可以迭代和递归方式实现,让我们进入实现细节:
前序遍历
下面是一颗树的前序遍历的样子:
1 | root node -> left node -> right node |
诀窍:
我们可以使用这个简单的技巧手动地找出任何树的前序遍历: 从根节点开始遍历整个树,保持自己在左边。
实现:
让我们深入研究这种遍历的实际实现。 1
2
3
4
5
6
7
8
9
10
11
12
```js
function walkPreOrder(root){
if(root === null) return
// do something here
console.log(root.val)
// recurse through child nodes
if(root.left) walkPreOrder(root.left)
if(root.right) walkPreOrder(root.right)
}
前序遍历的1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
```js
function walkPreOrder(root){
if(root === null) return
const stack = [root]
while(stack.length){
const item = stack.pop()
// do something
console.log(item)
// Left child is pushed after right one, since we want to print left child first hence it must be above right child in the stack
if(item.right) stack.push(item.right)
if(item.left) stack.push(item.left)
}
}
中序遍历
下面是一颗树的中序遍历的样子:
1 | left node -> root node -> right node |
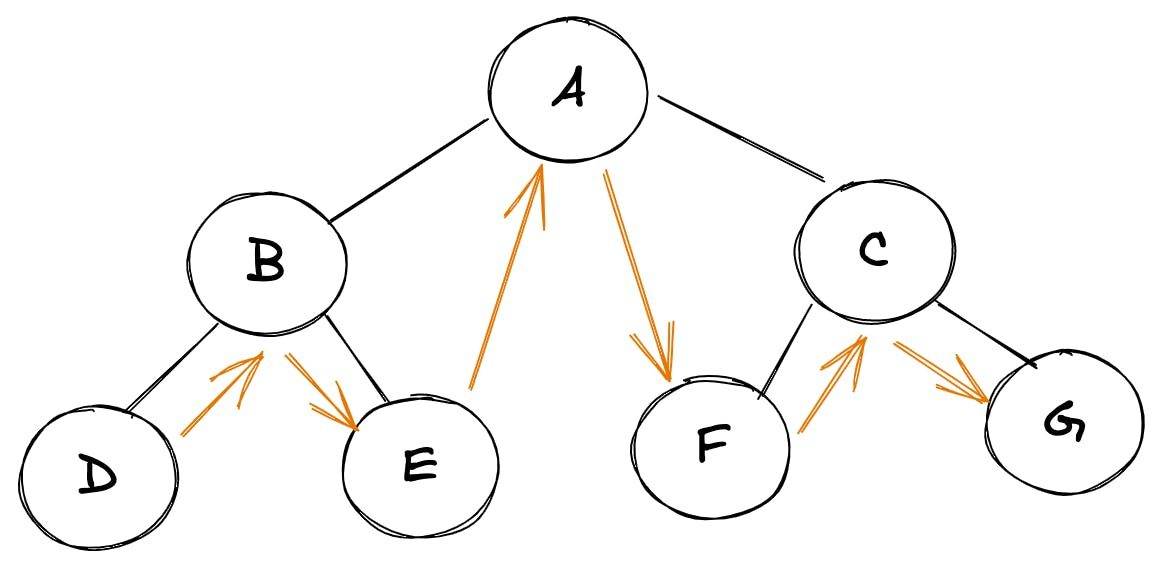
诀窍:
我们可以使用这个简单的技巧手动地找出任何树的中序遍历: 在树的底部水平放置一个平面镜像,并对所有节点进行投影。
实现:
递归:
1 | function walkInOrder(root){ |
迭代: 这个算法起初可能看起来有点神秘。但它相当直观的。让我们这样来看: 在中序遍历中,最左边的子节点首先被打印,然后是根节点,然后是右节点。所以我们首先想到的是:
1 | let curr = root |
在上述方法中,我们无法回溯,即返回到最左侧节点的父节点,所以我们需要一个堆栈来记录它们。因此,我们修订后的方法可能看起来如下:
1 | const stack = [] |
现在我们可以使用上面的方法来制定最终的迭代算法:
1 | function walkInOrder(root){ |
后序遍历
下面是一颗树的后序遍历的样子:
1 | left node -> right node -> root node |
诀窍:
对于任何树的快速手动后序遍历:一个接一个地提取所有最左边的叶节点。
实现:
让我们深入研究这种遍历的实际实现。
递归:
1 | function walkPostOrder(root){ |
迭代:我们已经有了用于前序遍历的迭代算法。 我们可以用那个吗? 由于后序遍历似乎只是前序遍历的逆序。 让我们来看看:
1 | // PreOrder: |
这里有一个细微的区别。但是我们可以通过稍微修改前序算法,然后对其进行逆序,从而得到后序结果。总体算法如下:
1 | // record result using |
使用与上面的迭代前序算法类似的方法,使用临时
1
+ 唯一的例外是我们使用 ```root-> right-> left``` 而不是 ```root-> left-> right
将遍历序列记录在一个数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
+ ```结果```的逆序给出了后序遍历
```js
function walkPostOrder(root){
if(root === null) return []
const tempStack = [root], result = []
while(tempStack.length){
const last = tempStack.pop()
result.push(last)
if(last.left) tempStack.push(last.left)
if(last.right) tempStack.push(last.right)
}
return result.reverse()
}
额外:JavaScript 提示
如果我们可以通过以下方式遍历树该多好:
1 | for(let node of walkPreOrder(tree) ){ |
看起来真的很好,而且很容易阅读,不是吗? 我们所要做的就是使用一个 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
以下是我们如何修改上面的 ```walkPreOrder``` 函数,使其按照上面共享的示例运行:
```js
function* walkPreOrder(root){
if(root === null) return
const stack = [root]
while(stack.length){
const item = stack.pop()
yield item
if(item.right) stack.push(item.right)
if(item.left) stack.push(item.left)
}
}
推荐理由
本文(配有多图)介绍了树结构在 JavaScript 语言里面如何遍历,写得浅显易懂,解释了广度优先、深度优先等多种方法的实现,翻译难免有出入,欢迎斧正!

